Cuatro detenidas por lucrarse con una menor que se prostituía
Las mujeres le facilitaron dos `pisos-mueblé? en el barrio del Raval sin licencia municipal
China prohíbe la importación de productos agrícolas y alimentos de Fukushima
China asegura que prohíbe las importaciones de estos productos "por haberse detectado contaminación radiactiva"
Dos detenidos por un tiroteo en una zona infantil de Sevilla un día de fiesta
Los acusados son delincuentes con numerosos antecedentes
Los vídeos de la NBA
Los vídeos de la NBA
Fitch rebaja la nota de la filial lusa del Santander
La sociedad justifica el recorte por los problemas de financiación en el mercado mayorista

GP de Australia: Entrenamientos Libres - F1 2011
McLaren domina en Melbourne. <p><strong>Especial: <a href="http://www.elpais.com/deportes/formula1/">Mundial de Fórmula 1</a></strong> </p>
Detenidos tres empresarios por supuesta explotación de trabajadores sin papeles
La Guardia Civil les achaca el impago de salarios y discriminación
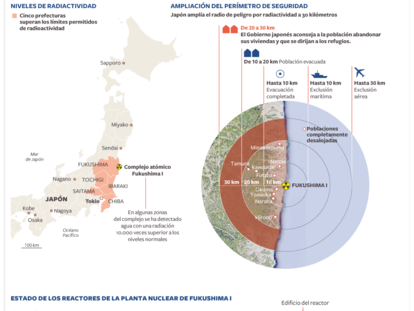
Estado de los reactores de la planta nuclear de Fukushima I
Esperanza Aguirre inaugura el policlínico del hospital 12 de Octubre con dos años de retraso
El edificio, con más de 250 consultas, concentra la asistencia que no requiere ingreso
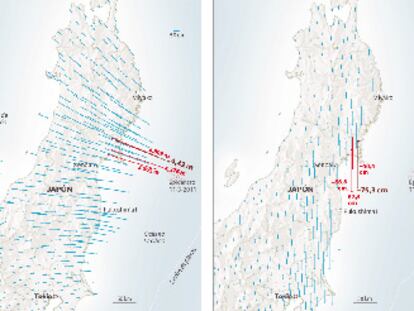
Japón amplía el radio de peligrosidad por radiactividad a 30 km de la central de Fukushima
El Ejército de EE UU proveerá de agua para refrigerar Fukushima.- El reactor 3 podría presentar una fisura.- Dos viajeros procedentes de Tokio llegan a China con niveles de radiación "seriamente excesivos"
EU denuncia ante la fiscalía los contratos y pagos del Consell a Calatrava
La coalición pide que se investiguen posibles delitos de prevaricación, malversación de fondos públicos y fraude
Los DVD de la semana
Llegan 'The town', con Ben Affleck a la dirección y 'Los ojos de Julia¡'
El Teatro Principal de Terrassa vuelve a subir el telón
Tras 4 años de reforma y 11 millones de euros invertidos, el nuevo teatro cuenta con 4.530 m2 de superficie y una sala con 623 butacas
A espiral infinita do viaxeiro Antón Lamazares
O novo Museo de Pontevedra abre cunha gran exposición retrospectiva do pintor galego máis universal
Epidemia musical en Hollywood
Hugh Laurie ('House') se une a la lista de actores que se pasan con mayor o menor éxito a la música
Tribuna: Desde el banquillo
El portavoz socialista valenciano, Ángel Luna, que será juzgado por denunciar el 'caso Gürtel', compara su proceso con el que narró Kafka
Google retrasa la apertura del código del nuevo Android
Aunque el sistema operativo es abierto, la empresa considera que no está a punto para que los desarrolladores hagan sus propias vesiones
Daniel Peña, reelegido rector de la Carlos III
El catedrático de Estadística logra el 50,98% del voto, frente al 49,02% de Luciano Parejo
Aragón se suma a Andalucía y aprueba una ley de muerte digna
La norma sale adelante con el único rechazo del Partido Popular.- Reconoce el derecho del paciente terminal a rechazar un tratamiento y no regula la objeción de conciencia de los profesionales sanitarios

Más pobres, pero también menos emprendedoras que los hombres
Festival 'twittero' por una buena causa
Además de Barcelona, Bilbao, Madrid y San Javier acogieron también el 'Twestival'

Una hormiga amenazada
<a href="http://www.fblasco.com/" target="blank">Fernando Blasco</a>, profesor de la <a href="http://www.upm.es/institucional" target="blank">Universidad Politécnica de Madrid</a>, presenta nuestro segundo desafío matemático. Coincidiendo con el <a href="http://www.rsme.es/centenario/" target="blank">centenario de la Real Sociedad Matemática Española</a>, EL PAÍS planteará un problema cada semana a sus lectores. <p> </p><p> NOTA IMPORTANTE: Por si queda alguna duda de la formulación del problema y a petición también de los lectores sordos, incluimos aquí el enunciado por escrito. Una hormiga se desplaza sin parar por las aristas de un cubo. Parte del vértice marcado con el número 1 (ver dibujo del profesor Blasco en la pizarra) por una de las tres aristas que salen de ese punto (con probabilidad 1/3 de tomar cualquiera de los caminos). Cada vez que llega a un nuevo vértice prosigue su paseo por una de las tres aristas que convergen en ese punto (vuelve para atrás, tira para un lado o para el otro), de nuevo con probabilidad 1/3 de tomar cada una de las rutas. </p><p> Los vértices 7 y 8 (ver dibujo en la pizarra) se rocían de insecticida, que es el único método que hay para matar a la hormiga: si el insecto llega a cualquiera de ellos morirá fulminantemente. Se pregunta: Partiendo del vértice 1. ¿Qué probabilidad hay de que la hormiga no muera nunca? ¿Qué probabilidad hay de que muera en el vértice 7? ¿Y en el 8?</p>
Una hormiga amenazada
La construcción de vivienda libre vuelver a caer en 2010
Las viviendas libres iniciadas en 2010 bajaron un 21,4%, frente al 66,28% que descendieron en 2009
Sófocles, nuestro contemporáneo
El dramaturgo y director de origen libanés Wajdi Mouawad ofrecerá tres obras del trágico en el Grec