15 de diciembre de 2011

Holanda prohibirá a los visitantes extranjeros consumir marihuana en los ‘coffeeshops‘

El Parlamento andaluz rechaza por décima vez crear una comisión de investigación

El cuadragésimo y último de los desafíos con los que hemos celebrado el <a href="http://www.rsme.es/centenario/" target="blank">centenario de la Real Sociedad Matemática Española</a> lo presenta Adolfo Quirós, profesor de la <a href="http://www.uam.es/ss/Satellite/es/home" target="blank">Universidad Autónoma de Madrid</a> y coordinador desde la RSME de esta iniciativa. Manda tu solución antes de las 00.00 horas del martes 20 de diciembre (medianoche del lunes, hora peninsular española) a <a href="mailto:problemamatematicas@gmail.com">problemamatematicas@gmail.com</a> y participa en el sorteo entre los acertantes de <a href="http://www.elpais.com/promociones/matematicas/">una biblioteca matemática</a> como la que cada domingo distribuye EL PAÍS en el quiosco.<p></p><p> A continuación, para aclarar las dudas y <b>en atención a nuestros lectores sordos</b>, añadimos el enunciado del problema por escrito. </p><p> Queremos transmitir un mensaje secreto. Para eso vamos a transformar un texto, que está escrito en el alfabeto castellano de 27 letras, de la A a la Z (incluyendo Ñ y W), en otro texto que se escribe usando solo 9 símbolos: los números del 1 al 9. Veamos como lo hacemos y lo ilustraremos con dos ejemplos. </p><p> Primero numeramos las letras por orden del 0 al 26, A=0, B=1, C=2, D=3,..., N=13, Ñ=14,..., W=23, X=24, Y=25, Z=26. Por ejemplo: </p><p> HOLA-> 7,15,11,0 </p><p> PEDRO->16,4,3,18,15 </p><p> A continuación escribimos cada uno de esos números como un número de tres cifras en base 3. Recordemos lo que esto quiere decir: Los números los escribimos normalmente en base 10, usando unidades (1=10^0), decenas (10=10^1), centenas (100=10^2), etc. Así, 3418 representa el número 3x10^3 + 4x10^2 + 1x10 + 8. Para escribir en base 3 usamos potencias de 3, y sólo necesitamos las cifras 0, 1 y 2. Por ejemplo, la expresión 212 en base 3 representa la cantidad 2x3^2+1x3+2, que en base 10 se escribiría como 23. </p><p> Nuestras letras quedarán entonces representadas por A=000, B=001, C=002, D=010, ..., N=111, Ñ= 112,..., W=212, X=220, Y=221, Z=222. Siguiendo con nuestros ejemplos: </p><p> HOLA-> 7,15,11,0 -> 0 2 1 1 2 0 1 0 2 0 0 0</p><p> PEDRO->16, 4, 3, 18, 15 -> 1 2 1 0 1 1 0 1 0 2 0 0 1 2 0</p><p> Obsérvese que hemos escrito 3 cifras por cada número (no hemos quitado los ceros a la izquierda) y, también, que hemos escrito todos los números seguidos, sin las comas que los separaban antes. Ahora viene la parte <i>secreta</i>. Haciendo algo que no os vamos a decir, porque descubrirlo es precisamente el desafío, transformamos finalmente nuestros textos en otros escritos usando sólo los números del 1 al 9. En los ejemplos: </p><p> HOLA-> 7, 15, 11, 0 -> 0 2 1 1 2 0 1 0 2 0 0 0 -> 3 5 7 4 7 1</p><p> PEDRO->16, 4, 3, 18, 15 -> 1 2 1 0 1 1 0 1 0 2 0 0 1 2 0 -> 6 4 5 2 3 1 6 1</p><p> El desafío consiste en leer el siguiente mensaje, que ha sido cifrado usando el procedimiento que hemos descrito, incluida la parte secreta: </p><p> 4 7 1 7 5 4 1 3 3 2 5 4 1 3 3 3 7 3 1 3 2 2 6 2 7 7 1 5 4 1 7 9 4 1 2 3 7 1 5 2 1 5 2 2 7 7 1 </p><p> <b>ALGUNAS OBSERVACIONES IMPORTANTES</b>. En el texto original no se utilizan signos de puntuación, acentos, ni siquiera los espacios entre palabras, que serían otro símbolo. Una buena idea es ir probando los procedimientos que se os ocurran en los dos ejemplos. Estrictamente hablando, el procedimiento es ligeramente distinto si el texto original tiene un número par o impar de letras, pero la diferencia no influye en nada en cómo leer los mensajes, es una cuestión puramente técnica que resultará evidente a posteriori. <b>Se considerará válida cualquier solución que haya sido capaz de descifrar el código y dé el mensaje correcto, pero, como siempre, nos gustaría saber cómo habéis llegado a ella</b>. </p><p> <a href="http://www.elpais.com/articulo/sociedad/desafios/matematicos/elpepusoc/20110712elpepusoc_8/Tes">DESAFÍOS ANTERIORES Y SUS SOLUCIONES</a></p>

Van Rompuy habla de "problemas electorales" un día después de que el Parlamento Europeo pidiese la repetición de los comicios por fraude

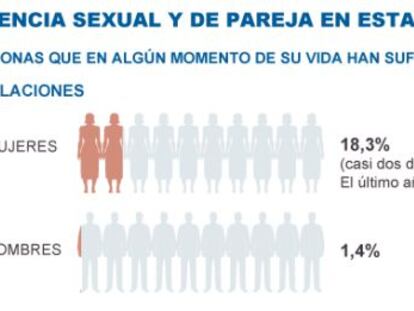
Casi una de cada cinco mujeres en EE UU declara haber sufrido un asalto sexual en su vida Más de la mitad señala a su pareja como agresor La mayoría no denuncia para evitar el estigma

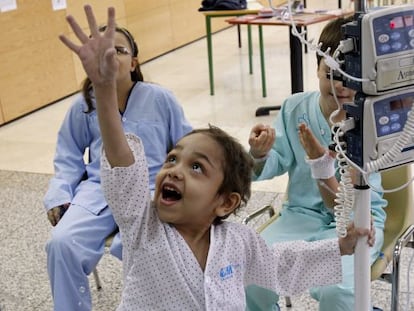
El Hospital Universitario de la Paz empezó a hacer trasplantes pediátricos hace 26 años Los pacientes, padres y médicos se han reunido para celebrar el primer millar

Un estudio concluye que el efecto nocivo de los vehículos en la salud supera al de la industria El tráfico puede elevar alrededor del 6% la mortalidad diaria por encima de la media

Fundó el diario 'El Sol', y luego 'La Voz', y antes la editorial Calpe Las cartas, notas y fotos del empresario Nicolás María de Urgoiti ya están en el archivo regional

Señala que si no puede cumplir algo de lo que prometió, lo explicará

Los barceloneses Brighton 64 cierran mañana en la sala Sol la gira de su 30º aniversario. Y nos recuerdan que, ajena al desgaste de las modas, la estética que defendieron mantiene su capacidad de fascinación